Copyright © 2014 by Hans Klaver, The Netherlands
RPN, postfix notation or stack logic, the calculator logic system used in many Hewlett-Packard (HP) calculators and simulations thereof, like the standard Calculator of macOS in RPN-mode (start with ⌘R or Command+R), is easy to use and saves you time because there is no need to use brackets or =. What’s better, it gives you more insight into your
calculations than using the ‘algebraic’ systems used by other calculators and it keeps you and not your calculator (see Appendix D) in command of what is calculated.
In 1972, more than 50 years ago, HP launched the HP‑35, the first pocket calculator with transcendental functions and the first with RPN. This same RPN is used in calculators sold by HP nowadays, like the HP‑12C,
HP‑12C Platinum,
HP‑15C Collector’s Edition,
HP 17bII+ and HP 35s, in all calculators sold by
SwissMicros,
also in the amazing WP 34S and WP 31S, and in a slightly modified version in the HP 20b and 30b and in graphing calculators like the HP 50g and HP Prime. This tutorial is a tribute to the HP‑35 and especially to the lay-out of the beautiful and informative HP‑35 Operating Manual. As far as possible it uses the colours of the keys as they appear in that Manual, so the colours of your calculator’s keys will almost always differ; don’t get confused by that.
The ‘Cheat Sheet’ below serves as a table of contents and as a summary for this tutorial.
You can learn the basics of RPN (1., 2., 3. & 4. of the Cheat Sheet) in less than 15 minutes. The finer details (5., 6. & 7.) take another 30 minutes to get used to. Understanding of 8. is a bit more difficult and probably is unnecessary, but if you are a real ‘formula cruncher’ study of that point will be well paid off.
The Appendices elaborate on a few interesting points.
How to practice?
To get a feeling for the HP‑35 you could use Neil Fraser’s JavaScript HP‑35 simulator; or my modification of it, the HP‑35 SOS, which has ‘Stack Overflow Sensing’. With Neil Fraser’s
HP‑35 simulator you can only use a pointing device (e.g. mouse) to press the calculator keys; with my
HP‑35 SOS you can also use your computer keyboard.
If you don’t have a hardware RPN calculator use your computer keyboard and practice on the famous HP‑15C with the online version of Greg Hewgill’s HP‑15C simulator. With this simulator you can watch the stack live! Open in a separate window on macOS by simultaneously pressing ⌥⌘ (option+command) while clicking the link; or on Windows, macOS or Linux right-click the link and choose ‘Open in a separate window’.
You can also download one of the numerous RPN calculator programs for your computer or smartphone. E.g. the HP Prime emulator for Windows or macOS; the HP 35s emulator for Windows or Wine; the WP 34S emulator for Windows, macOS, Linux or iOS; or Free42, an HP-42S simulator, available for Android, iOS, Windows, macOS and Linux; Free42 also features a simulator of the HP-82240 printer.
If you’re a fan of the command-line, you could also use the ‘desk calculator’ utility dc, one of the oldest UNIX programs, even predating C.
In Linux and macOS dc is installed already; Windows users can try out an online dc
Note that using dc you’ll have to press p⏎ to see the result of a calculation, but apart from that for basic arithmetic (1. through 5. of the Cheat Sheet) the keystrokes are quite similar to those used in this tutorial (use * to multiply, / to divide, v for the square root function √x and ^ for the power function yx ). If your results are not as expected see appendix H.
RPN Cheat Sheet
-
One-number calculations (such as 1/x, √x, x2, cos x, log x): first key-in the number, then press the function key (or press the applicable prefix (‘shift’) key, then the function key).
Example: calculate √2 Press: 2 √x Result:1.41421356237
Example: calculate 342 Press: 34 x2 Result:1156
-
Two-number calculations (+, –, ×, ÷, yx, %, ∆%, %T ): key-in the first number, press ENTER to separate the first number from the second, key-in the second number (do not press ENTER after the second number!)*, then press the function key.
Example: calculate 12 + 3 Press: 12 ENTER↑ 3 + Result:15
-
Series of additions and/or subtractions (like 12 + 34 + 56 – 78 + 90 – 12): ENTER should only be used to separate two numbers keyed-in without a function key in-between (in this case between the first and the second number), all other numbers are separated by the function keys (which also save the intermediate results).
12 ENTER↑
34 + 56 + 78 – 90 + 12 –
Result:102
There is no limit to the number of additions and/or subtractions that can be done in a row.
-
Chain calculations, for example (12 × 34) + (56 × 78) – (90 × 12): work them as on paper, like so
12 ENTER↑ 34 ×
56 ENTER↑ 78 × +
90 ENTER↑ 12 × – Result:3696
There is no limit to the number of operations that can be done in a row when there is only one level of parentheses, provided that all parentheses have been placed correctly to indicate the order of precedence of all operations.
-
Calculations with nested parentheses like 3 × (4 + (5 × (6 + 7))): begin with the innermost set of parentheses and work outwards. With this technique nearly every complicated calculation can be done on a 4-level stack RPN-calculator.
6 ENTER↑ 7 + 5 × 4 + 3 × Result:207
Calculations like the one above cannot be done in a pure left-to-right way on a calculator with a 4-level stack because more than 4 numbers have to be keyed-in before the first operation key is pressed.
-
Use of x
 y or ► or
y or ► or  in nested calculations. To get the order of the numbers right when you have to do a non-commutative operation (–, ÷, yx ) ‘backwards’, just before pressing the operation key press x
in nested calculations. To get the order of the numbers right when you have to do a non-commutative operation (–, ÷, yx ) ‘backwards’, just before pressing the operation key press x y (‘exchange x and y’). In the HP 20b/30b this is the
y (‘exchange x and y’). In the HP 20b/30b this is the
 key. In HP graphing calculators use SWAP: before the operation key press ENTER followed by ► or
key. In HP graphing calculators use SWAP: before the operation key press ENTER followed by ► or
 (
(  ).
).
E.g.: 3 × (4 – (5 × (6 + 7)))
6 ENTER↑ 7 + 5 × 4 x y
– 3 × Result:–183
y
– 3 × Result:–183
Beware of the order of operations when there are several additions and subtractions or multiplications and divisions next to each other!
(see explanation).
-
Use of STO and RCL . If you’re not sure that the 4-level stack will be enough then use additional memory with STO and RCL . When there is a non-commutative operation (–, ÷, yx ) somewhere in the middle of the formula, start with the part after this operation, STOre the intermediate result, and when the part before this operation is done, RCL (recall) the intermediate result and press the middle operation key. In this way you get the order of the numbers right without using x
 y, so you save one keystroke.
y, so you save one keystroke.
E.g.: (29 + 38)(47 + 56) – (65 + 74)(83 + 92)
First think what this actually means:
[(29 + 38) × (47 + 56)] – [(65 + 74) × (83 + 92)]
There are implied parentheses around each term of this calculation and that’s why this isn’t an example with only one level of parentheses (see 4.), so you aren’t sure whether the 4-level stack will be enough for this calculation (actually it isn’t). The easiest way to solve this one is by starting after the minus – :
6 ENTER↑
5 y x
7 ENTER↑
4 y x
+
8 ENTER↑
3 y x
9 ENTER↑
2 y x
+
×
STO†
2 ENTER↑
9 y x
3 ENTER↑
8 y x
+
4 ENTER↑
7 y x
5 ENTER↑
6 y x
+
×
RCL
–
Result:220,364,696
-
How to recognize and handle calculations that cannot be done using a 4‑level stack?
• Obviously the 4-level stack has only four storage locations, holding the number in the display and three additional numbers. These four numbers can either be newly keyed-in numbers, or intermediate results from calculations or any combination thereof, but the total may never exceed four!
• When you use ENTER↑ once to key-in two new numbers only two intermediate results from previous operations will be preserved.
Keeping these two rules in mind a simple counting technique suffices to recognize calculations that cannot be done using only the 4-level stack. When you always start calculations from within the innermost set of parentheses such situations will rarely arise. But when they do arise you can always handle them using additional memory with STO and RCL .
*
If you do press ENTER after the second number you get wrong results on classical RPN calculators! On the recent models HP 20b and 30b and on the graphing HP calculators like the series 28, 48 & 49 and the 50g and Prime (which use a variant of RPN called Entry RPN or RPL) it is allowed to press ENTER after the second number, but it is not necessary. See Appendix A. The Stack and Appendix G. RPN Variants.
†
The HP-35 had only one additional memory location apart from the stack; later models need a register number or letter after STO and RCL , e.g.: STO 1 and RCL 1 .
Basics of RPN
- Principles.
RPN is based upon four leading principles:
-
The number or two numbers necessary for an operation (calculation) should be in the calculator before an operation key (operator) is pressed. So the order is always: first number(s), then operator.
-
The result of every operation immediately appears in the display and overwrites the original number or two numbers within the calculator.
-
The result of every operation can be used by a next operation and is stored automatically when a new number is keyed-in.
-
Only when two new numbers have to be keyed-in before the next operation can be done, the two numbers should be separated from each other by a special key: ENTER↑.
-
One number calculations.
The order of entering numbers and operations in RPN can easiest be seen with single number functions. No matter if you write the math operator in front of the number (like in √x or log x or 1/x) or behind the number (like in x2 or x!), when using an RPN calculator the order of calculations is always: first number, then operator.
Try the examples below. It is not necessary to clear the number in the display (‘x’) between two different calculations, because numbers present in the calculator as a result of a previous operation are ‘pushed upwards’ (and can be used later in a calculation if necessary). If you would make an entry mistake, you can use CL x (Clear x) or  (Backspace) and retype the number correctly.
(Backspace) and retype the number correctly.
Example I: √169 (the square root of 169)
| Press |
Display |
Comments |
| 169 |
169 |
| √x |
13 |
Example II: 9! (the factorial of 9 = 1 × 2 × 3 × 4 × 5 × 6 × 7 × 8 × 9)
* The HP-35 had one prefix key: ARC. Most later models have several. They have interesting nicknames:
‘gold’, f
‘fold’, f-1
‘dolf’, ‘blue’, g ‘glue’, h ‘hack’. Also HYP and HYP-1 are (shifted) prefix keys.
| Press |
Display |
Comments |
| 9 |
9 |
| x ! |
362,880 |
One-number operations always act upon the number in the display, called x, and the result of the operation overwrites this number and becomes the new x. This new x can be used as the argument of another one-number operation (or as one of the two arguments of a two-number operation).
| Press |
Display |
Comments |
| 121 |
121 |
| √x |
11 |
|
1/x |
0.09090909091 |
For an explanation of the workings of the stack in one number calculations see
here in Appendix A.
- Two-number calculations.
RPN treats problems the way you do on paper.
For example, you would solve 456 + 123 like this:
456
123
——— +
579
The sequence is: 456 123 +
This is the same order followed when using RPN calculators: key-in the first number, 456, then press ENTER↑ to tell the calculator that you have completed the first number and that you want to enter a second number, then key-in the second number, 123, and press + to add both numbers. The answer,579, immediately appears in the display when you press + ; both original numbers disappear from the calculator and are replaced by the result.
The same is true for other operations on two numbers like – (subtraction), × (multiplication), ÷ (division), and yx (exponentiation or ‘power’ function: the number keyed-in first (y) raised to the power of the second number (x)). Try it!
456 456 456
123 123 ——— = 3.707317073 3-10 = 0.00001693508781
——— – ————— × 123
333 56088
Example IV: 456 – 123
| Press |
Display |
Comments |
| 456 |
456 |
| ENTER↑ |
456 |
| 123 |
123 |
| – |
333 |
Example V: 456 × 123
456 ENTER↑ 123 × Answer: 56,088
Example VI: 456/123
456 ENTER↑ 123 ÷ Answer: 3.70731707317
Example VII: 3–10
* On some models +/–
† The HP-35 is the only early model with a x y key, and there the exponent is keyed-in first. Unlike all other models the HP Prime has a key labelled xy, which operates like the y x key in the example.
| Press |
Display |
Comments |
| 3 |
3 |
| ENTER↑ |
3 |
| 10 |
10 |
| CH S * |
–10 |
| y x† |
0.00001693508781 |
Also percentage operations (%, ∆% and %T) are two-number calculations.
Example VIII: What is 21% of 367 billion?
* Exact powers of ten are easy to key-in, e.g. 1 million = 106: E EX 6 and 0.0001 = 10-4: E EX 4 CH S
| Press |
Display |
Comments |
| 367 E EX 9 |
367 09 |
| ENTER↑ |
3.670,000 11 |
| 21 |
21 |
| % |
7.707,000 10 |
See Appendix C for more examples of percentage calculations.
For an explanation of the workings of the stack in two number calculations see
here in Appendix A.
- Serial calculations like 12 + 34 + 56 – 78 + 90 – 12.
Another example that the result of an operation is itself used by the next operation is the calculation of the square root of an addition: √(12 + 34). First do the addition: 12 ENTER↑ 34 + and when the intermediate result 46 is in the display press the √x button to perform the square root function. Result:6.782329983
In the same way the result of an addition can be used by another addition, and the next result by yet another addition, etc.
To add the three numbers 12, 34 and 56 you simply press:
12 ENTER↑
34 +
56 + . Result:102. Next you can do a subsequent addition by keying in the number and press + , or a subsequent subtraction by keying in a number followed by – . There is no limit to the number of additions or subtractions you can do in one row.
Example IX: 12 + 34 + 56 – 78 + 90 – 12
| Press |
Display |
Comments |
| 12 ENTER↑ |
12 |
| 34 + |
46 |
| 56 + |
102 |
| 78 – |
24 |
| 90 + |
114 |
| 12 – |
102 |
The ENTER↑ key is used to separate two numbers entered immediately after each other, such as the first two numbers; all following numbers are separated by the operation keys (in this case + or – ), which also automatically save the calculated (or intermediate) results.
- Chain calculations
Now look at this problem with parentheses:
(56 × 78) – (12 × 34)
If you solved it on paper, you would first multiply 56 × 78, then 12 × 34, then subtract the two intermediate results to get the final result. That’s just the way you do it using an RPN-calculator, without the need to key-in the parentheses. In this calculation you must use ENTER↑ two times since you must key-in another pair of numbers before you can perform a function.
Example X: (56 × 78) — (12 × 34)
| Press |
Display |
Comments |
| 56 ENTER↑ |
56 |
| 78 × |
4368 |
| 12 ENTER↑ |
12 |
| 34 × |
408 |
| – |
3960 |
Note that you only have to press ENTER↑ to separate two numbers that are keyed-in without an operation key in-between. The intermediate results are automatically saved in the calculator for you! Just as you would work out the problem with paper and pencil, you solve what’s within the parentheses first and subtract – last. The stack memory ‘automagically’ retrieves the intermediate results for the final subtraction operation.
Mixed one- and two-number operations follow the same principle: first key-in the number(s), then the operation(s); no parentheses, no ‘equals’ (=) key to press, the same order you would use on paper. For example:
Example XI: (13 + 8) × log 100
| Press |
Display |
Comments |
| 13 ENTER↑ |
13 |
| 8 + |
21 |
| 100 |
100 |
| LOG |
2 |
| × |
42 |
Another example of mixed one and two-number operations; again the intermediate results are saved automatically:
Example XII: 232 – (13 × 9) + (5/7)
| Press |
Display |
Comments |
| 23 x2 |
529 |
| 13 ENTER↑ 9 × |
117 |
| – |
412 |
| 5 ENTER↑ 7 ÷ |
0.714285714286 |
| + |
412.714285714 |
There is no limit to the number of operations that can be done in a row when there is only one level of parentheses, provided that all parentheses have been placed correctly to indicate the order of preference of all operations.
Finer details of RPN
- Nested calculations
Also calculations with nested parentheses are best worked the same way you would use on paper, in which case there is no other way than to begin at the innermost set of parentheses, and work outwards. Consider the following calculation:
3[4 + 5(6 + 7)]
First think what this actually means: 3 × [4 + (5 × (6 + 7))]
Example XIII: 3 × [4 + (5 × (6 + 7))]
| Press |
Display |
Comments |
| 6 ENTER↑ 7 + |
13 |
| 5 × |
65 |
| 4 + |
69 |
| 3 × |
207 |
Doing a calculation starting at the innermost set of parentheses and working outwards has several advantages:
- It takes fewer keystrokes than working from left to right.
- It is easier to keep track of what you are doing.
- It requires fewer registers on the stack. This is very important when using an RPN calculator with a 4‑level stack (all HP RPN calculators except the HP graphing calculators of the series 28, 48 and 49, the HP 50g and Prime; also the WP 31S and WP 34S in 8‑level stack mode are an exception). Working the above calculation in a left-to-right order with a 4‑level stack machine will overflow the 4‑level stack and give a wrong result (without warning…). The above mentioned graphing calculators have a virtually unlimited stack and are immune to this problem.
Example XIV: 3 × [4 + (5 × (6 + 7))]. Alternative method 1: pure left-to-right order.
This method takes more keystrokes than the method used in example XIII. It only gives a correct result when the RPN-stack has at least 5 levels; it gives a wrong result on 4‑level stack RPN calculators due to stack overflow!
* A 4-level stack RPN calculator will give the wrong answer 276 (= 4 × 69).
| Press |
Display |
Comments |
| 3 ENTER↑ |
3 |
| 4 ENTER↑ |
4 |
| 5 ENTER↑ |
5 |
| 6 |
6 |
| ENTER↑ |
6 |
| 7 |
7 |
| + |
13 |
| × |
65 |
| + |
69 |
| × |
207 |
For an explanation of the workings of the stack in nested calculations see
here in Appendix A.
Example XV: 3 × [4 + (5 × (6 + 7))]. Alternative method 2: partial left-to-right order.
This method gives a correct result on all RPN calculators, including 4-level stack models.
| Press |
Display |
Comments |
| 4 ENTER↑ |
4 |
| 5 ENTER↑ |
5 |
| 6 ENTER↑ |
6 |
| 7 |
7 |
| + |
13 |
| × |
65 |
| + |
69 |
| 3 × |
207 |
It is obvious that both left-to-right methods take more keystrokes than the preferred method, working from the innermost set of parentheses outwards, which in addition gives you a better overview of the intermediate results. And on a 4‑level stack machine the left-to-right method of nested calculations can easily lead to stack overflow, giving wrong results without warning. So use the left-to-right method for calculations with nested parentheses only when you know exactly what you are doing! Below are some hints on how to recognize nested calculations that can and cannot safely be done in a left-to-right manner.
-
Use of x y or ► or
y or ► or  in nested calculations.
in nested calculations.
When doing nested calculations from the innermost set of parentheses outwards you will often have to do a non-commutative operation (–, ÷, yx ) ‘backwards’, so that the order of the numbers would be wrong. Getting the order of the numbers right can often best be done using the x exchange y key x y (in graphing calculators called SWAP, accessed with the right arrow key ►; in the HP 20b, 30b and HP Prime the key has a symbol like this:
y (in graphing calculators called SWAP, accessed with the right arrow key ►; in the HP 20b, 30b and HP Prime the key has a symbol like this:  ). This key exchanges the number in the display (called x) with the number in the second stack level (called y). In these cases x
). This key exchanges the number in the display (called x) with the number in the second stack level (called y). In these cases x y or ► or
y or ► or  should be pressed immediately before pressing the –, ÷ or y x key. In most HP graphing calculators SWAP only works when there is no command line or (in the Prime) when the entry line is empty, so you might have to press ENTER before ► or
should be pressed immediately before pressing the –, ÷ or y x key. In most HP graphing calculators SWAP only works when there is no command line or (in the Prime) when the entry line is empty, so you might have to press ENTER before ► or  (
(  ).
).
Example XVI: 3 × [4 – (5 × (6 + 7))]
* In graphing calculators you will often have to put the 4 on the stack with an extra ENTER before you can use the SWAP function by pressing ► or  .
.
| Press |
Display |
Comments |
| 6 ENTER↑ 7 + |
13 |
| 5 × |
65 |
4 x y y |
65 |
| – |
–61 |
| 3 × |
–183 |
| Example XVII: |
|
4 |
|
|
14 + (7 × 3) – 2 |
* In graphing calculators you will often have to put the 4 on the stack with an extra ENTER before you can use the SWAP function by pressing ► or  .
.
| Press |
Display |
Comments |
| 7 ENTER↑ 3 × |
21 |
| 14 + 2 – |
33 |
4 x y y |
33 |
| ÷ |
0.121212121212 |
You could have done the above calculation by using 1/x after ÷ or by changing the division into a multiplication of the reciprocal (multiplicative inverse) using 1/x and ×. Likewise you could have done Example XVI by using CH S after – or by changing the subtraction into an addition of a negative number (additive inverse) using CH S and +.
You even can do a power calculation ‘backwards’ by using inverse functions (exponential and natural logarithm) and the equivalence y x = e x ln y. So 7 5 can be calculated with
7 ENTER↑ 5 y x or with 5 ENTER↑ 7 LN × e x. But for most of us the latter method would be quite convoluted. Here too RPN offers a perfectly simple and easy to remember method:
7 5 ‘backwards’ using x y: 5 ENTER↑ 7 x
y: 5 ENTER↑ 7 x y y x Answer: 16,807
y y x Answer: 16,807
Using x y (or SWAP with ► or
y (or SWAP with ► or  ) is a straightforward method which works for all non-commutative operations, including y x.
) is a straightforward method which works for all non-commutative operations, including y x.
But beware: using x y is not the same as using 1/x and × or using CH S and + !
y is not the same as using 1/x and × or using CH S and + !
These latter methods are ‘more universal’ in that they can be used safely for ‘backwards’ calculation of a series of multiplications and divisions or additions and subtractions.
Using x y you have to watch out carefully for the correct order of operations!
y you have to watch out carefully for the correct order of operations!
E.g.: 1 – 2 + 3 – [4 – (5 × (6 + 7))]
This would be the wrong way:
6
ENTER↑
7
+
5
×
4
x y
–
3
x
y
–
3
x y
–
2
+
1
x
y
–
2
+
1
x y
–
y
–
Answer: -65 Wrong!
Because a series of additions and subtractions should always be done from left-to right (see Appendix E) there are implied parentheses in this calculation:
1 – 2 + 3 – [4 – (5 × (6 + 7))] =
(1 – 2 + 3) – [4 – (5 × (6 + 7))]
So a correct way would be:
6
ENTER↑
7
+
5
×
4
x y
–
1
ENTER↑
2
–
3
+
x
y
–
1
ENTER↑
2
–
3
+
x y
– (17 key presses)
y
– (17 key presses)
Answer: 63
Using CH S and
+ you can do everything ‘backwards’ because addition is a commutative operation:
1 – 2 + 3 – [4 – (5 × (6 + 7))] =
1 + –2 + 3 + –[4 + –(5 × (6 + 7))]
6
ENTER↑
7
+
5
×
CH S
4
+
CH S
3
+
2
CH S
+
1
+ (17 key presses)
Answer: 63
The best and shortest way to do this calculation is to start at the left, and only when you encounter the nested parentheses work from the innermost parentheses outwards:
1
ENTER↑
2
–
3
+
6
ENTER↑
7
+
5
×
4
x y
–
– (16 key presses)
y
–
– (16 key presses)
Answer: 63
Doing the whole calculation from left-to-right is not shorter: it takes one more key press. And this technique can only be used when the stack hight of your calculator is sufficient (in this case at least 5), otherwise you get stack overflow and a wrong answer (without warning!).
1
ENTER↑
2
–
3
+
4
ENTER↑
5
ENTER↑
6
ENTER↑
7
+
×
–
– (17 key presses)
Answer: 63 (Note: a 4-level stack RPN calculator will give the wrong answer 65 ).
Example XVIII: 432
| Press |
Display |
Comments |
| 3 ENTER↑ 2 y x |
9 |
4 x y y |
9 |
| y x |
262,144 |
Example XIX: 432 (alternative solution, from left to right)
| Press |
Display |
Comments |
| 4 ENTER↑ |
4 |
| 3 ENTER↑ |
3 |
| 2 |
2 |
| y x |
9 |
| y x |
262,144 |
The next calculation can only be done ‘backwards’ on 4‑level stack RPN calculators, because from left to right there are 6 numbers (1, 1.001, ‑6.2, ‑2, 3, π) before we can do any operation. So first we will work the expression in the first exponent, then the base expression.
Example XX: 1 — 1.001(–6.2 — 23π)
* The HP-35 is the only HP pocket calculator with a separate key for π, so no ‘shift’ needed.
† The macOS Calculator does need ENTER before and after π and e, which may be considered a bug rather than a feature.
| Press |
Display |
Comments |
| 6.2 CH S ENTER↑ |
–6.2 |
| 2 ENTER↑ |
2 |
| 3 π |
3.14159265359 |
| × y x |
687.2913357 |
| – |
-693.4913357 |
1.001 x y y x y y x |
0.500001180 |
1 x y – y – |
0.499998820 |
The following calculation can be done both ways (left-to-right and ‘backwards’; explanation below under 7.):
Example XXI: (e – 1)2/(π–log π) (left-to-right)
* The macOS Calculator does need ENTER before and after π and e, which may be considered a bug rather than a feature.
† For an explanation of this duplicating property of ENTER see
Appendix A. The Stack.
| Press |
Display |
Comments |
| 1 e x |
2.71828182846 |
| 1 – |
1.71828182846 |
| 2 |
2 |
| π ENTER↑ |
3.14159265359 |
| LOG |
0.497149872694 |
| – |
2.6444427809 |
| ÷ |
0.756302996777 |
| y x |
1.50592241348 |
Example XXII: (e – 1)2/(π–log π) (alternative solution: ‘backwards’)
* The macOS Calculator does need ENTER before and after π and e, which may be considered a bug rather than a feature.
† For an explanation of this duplicating property of ENTER see
Appendix A. The Stack.
| Press |
Display |
Comments |
| 2 |
2 |
| π ENTER↑ |
3.14159265359 |
| LOG |
0.497149872694 |
| – |
2.6444427809 |
| ÷ |
0.756302996777 |
| 1 e x |
2.71828182846 |
| 1 – |
1.71828182846 |
x y y |
0.756302996777 |
| y x |
1.50592241348 |
- Use of STO and RCL when the 4‑level stack is not enough.
If you stick to the method of working calculations with nested parentheses from the innermost set of parentheses outwards then you will probably never encounter a calculation that cannot be done without overflowing a 4‑level stack. Nevertheless these calculations do exist, and below it is explained how to recognize them. It is easy to handle them using STO and RCL , so if you’re not sure whether the 4‑level stack will be enough don’t hesitate to make use of these keys.
The HP‑35 had only one additional memory register apart from the stack, so pressing STO was enough to copy the number in the display to this register. In all later HP calculators STO should be followed by one or two numbers to address a specified memory register. Pressing RCL , if necessary followed by a register number, copies the contents of this register back to the display. It is not necessary to use ENTER before or after RCL.
Keep in mind that use of STO and RCL reverses the order of the operation. This isn’t important in commutative operations (+, ×), but it is important in non-commutative operations (–, ÷, yx).
E.g.: 45 – 12
45 ENTER↑ 12 – Answer: 33
45 STO 12 RCL x y – Answer: 33
y – Answer: 33
12 STO 45 RCL – Answer: 33
So when you want to use STO and RCL in a long calculation start with the part after the subtraction or division to save one keystroke: x y .
y .
Example XXIII: 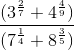 If you’re not sure that this one can be done on a 4-level stack, use STO and RCL .
If you’re not sure that this one can be done on a 4-level stack, use STO and RCL .
* The HP-35 had only one memory location apart from the stack; later models need a register number after STO and RCL.
| Press |
Display |
Comments |
| 7 ENTER↑ 1 ENTER↑ 4 |
4 |
| ÷ |
0.25 |
| y x |
1.62657656169779 |
| 8 ENTER↑ 3 ENTER↑ 5 |
5 |
| ÷ |
0.6 |
| y x |
3.4822022531845 |
| + |
5.10877881488228 |
| STO |
5.10877881488228 |
| 3 ENTER↑ 2 ENTER↑ 7 |
7 |
| ÷ |
0.28571428571429 |
| y x |
1.36873810664221 |
| 4 ENTER↑ 4 ENTER↑ 9 |
9 |
| ÷ |
0.44444444444444 |
| y x |
1.85174942457457 |
| + |
3.22048753121678 |
| RCL |
5.10877881488228 |
| ÷ |
0.63038304219303 |
Example XXIV: 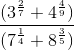 Actually this one can be done on a 4-level stack without using STO and RCL by doing the last term ‘backwards’.
Actually this one can be done on a 4-level stack without using STO and RCL by doing the last term ‘backwards’.
| Press |
Display |
Comments |
| 3 ENTER↑ 2 ENTER↑ 7 |
7 |
| ÷ |
0.28571428571429 |
| y x |
1.36873810664221 |
| 4 ENTER↑ 4 ENTER↑ 9 |
9 |
| ÷ |
0.44444444444444 |
| y x |
1.85174942457457 |
| + |
3.22048753121678 |
| 7 ENTER↑ 1 ENTER↑ 4 |
4 |
| ÷ |
0.25 |
| y x |
1.62657656169779 |
| 3 ENTER↑ 5 |
5 |
| ÷ |
0.6 |
8 x y y x y y x |
3.4822022531845 |
| + |
5.10877881488228 |
| ÷ |
0.63038304219303 |
- How to recognize and handle calculations that cannot be done using a 4‑level stack?
Figuring out if a calculation can be done without overflowing the 4‑level stack is a matter of counting. Sometimes the counting is easy, but sometimes it can be quite difficult. The simple counting technique explained below can even be used in the most complicated formulae.
Note that the following does not apply to the HP graphing RPN calculators (HP series 28, 48 and 49 and the HP 50g and Prime), because they have a virtually unlimited stack that is immune to overflow; also the WP 31S and WP 34S when operated in 8‑level stack mode will in practice hardly ever overflow.
First we will show two impressive calculations that can be done using only the automatic registers of a 4-level stack.
Example XXV:* 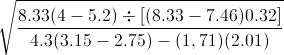
* This example premiered in the HP-11C Owner’s Handbook (1981) and can be found in several later Manuals.
| Press |
Display |
Comments |
| 4 ENTER↑ |
4 |
| 5.2 – |
–1.2 |
| 8.33 × |
–9.996 |
| LAST x |
8.33 |
| 7.46 – |
0.87 |
| 0.32 × |
0.2784 |
| ÷ |
–35.90517241 |
| 3.15 ENTER↑ |
3.15 |
| 2.75 – |
0.4 |
| 4.3 × |
1.72 |
| 1.71 ENTER↑ |
1.71 |
| 2.01 × |
3.4371 |
| – |
–1.7171 |
| ÷ |
20.910356074 |
| √x |
4.572784280 |
Example XXVI:* 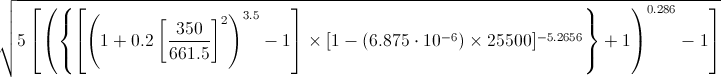
* This example first appeared in the HP-25 Owner’s Handbook (1975). It calculates the Mach number of an aeroplane flying with a calibrated airspeed (CAS) of 350 knots at a pressure altitude (PALT) of 25,500 feet.
| Press |
Display |
Comments |
| 350 ENTER↑ |
350 |
| 661.5 ÷ |
0.529100529 |
| x2 |
0.279947370 |
| 0.2 × 1 + |
1.055989474 |
| 3.5 y x 1 – |
0.210064617 |
| 1 ENTER↑ |
1.0 |
| 6.875 E EX 6 CH S |
6.875 –06 |
| ENTER↑ |
0.000006875 |
| 25500 × – |
0.824687500 |
| 5.2656 CH S y x |
2.759220911 |
| × |
0.579614684 |
| 1 + 0.286 y x |
1.139687100 |
| 1 – |
0.139687100 |
| 5 × √x |
0.835724536 |
Let’s try to figure out why the two complicated expressions above (the second one with 6 levels of parentheses!) do not overflow the 4‑level stack, while an innocent-looking expression such as 3[4 + 5(6 + 7)] goes awry when done in a left-to-right way.
There are a few simple principles you should remember in order to understand what goes on within the 4‑level stack during a calculation:
- The stack can hold only 4 numbers, the number in the display and 3 additional numbers. These 4 numbers can either be newly keyed-in numbers, or intermediate results from the calculation or any combination thereof, but the total may never exceed four!
- So when the stack is full with 4 numbers you need to make room before you can key-in a new number.
- The only way to make room on the stack is by doing a two-number operation (+, –, ×, ÷, yx) with two numbers already present on the stack: two numbers are removed in the operation, and make room for the result and a free place. So a two-number operation without entering any numbers makes room for one new number!
- One-number operations leave the rest of the stack unchanged, and the same goes for two-number operations with one newly keyed-in number and one number already on the stack, so on a full stack you can do an unlimited series of such operations. But to make room you must do one or a few two-number operations with both numbers already on the stack.
- When entering new numbers remember that you need only three ENTERs to enter four numbers: 1 ENTER↑ 2 ENTER↑ 3 ENTER↑ 4. In Classical RPN (but not in Entry RPN) machines when the stack is full only pressing ENTER↑ (without keying in a number) is enough to overflow the stack. This is because in Classical RPN (not in Entry RPN) machines ENTER↑ duplicates the number in the display (x) and pushes all numbers already in the stack upwards; in this action the number on the top of the stack is pushed ‘over the top’ and gets lost. A number subsequently keyed-in overwrites the number in the display and becomes the new x, but it is the ENTER that does the ‘pushing’ and so is responsible for the resulting overflow.
See Appendix A for a thorough description of the stack.
With this knowledge it can easily be seen why you cannot do 3[4 + 5(6 + 7)] purely from left to right. Only after having entered 5 numbers (3, 4, 5, 6 and 7) can you do a two-number operation, and when entering 5 numbers (4 ENTERs) in a row the first number entered (the 3) will get lost (see Example XIV). So you could do this calculation starting with the 4 and working from there to the right, and finally doing the first operation (see Example XV).
When doing this calculation starting with the innermost pair of parentheses you can do the first two-number operation right after having entered the first two numbers, so immediately one stack place is freed. From there you do another two-number operation right after each new number keyed-in. So in this way you need only 2 of the four stack levels during the whole calculation. Look here for an illustration of the workings of the stack during this calculation.
Some calculations can be done both ways: (e — 1)2/(π–log π)
After having calculated e — 1 (which leaves one result on the stack) you would have to push three additional numbers (2, π and π) on the stack. So this calculation can be done from left to right on a 4‑level stack. Of course you can also start from within the innermost set of parentheses, in this case the exponent, because this calculation could have been written thus: (e — 1)^(2/(π–log π)). But that would complicate things a bit, because of the two SWAPs ( x y or ►) you would have to do. See Examples XXI and XXII.
y or ►) you would have to do. See Examples XXI and XXII.
Now, let’s have a look at a calculation that is too much for the 4‑level stack, no matter how you attack it. They’re hard to find, but I found one (thanks to the HP Forum on the Museum of HP Calculators). Another one can be seen in the Cheat Sheet under 7. In both calculations you will have to use STO and RCL to get the right answer on a 4‑level stack RPN calculator:
[(3+1)(4+3) + (2+6)(4+6)] / [(2+3)(2+1) + (3+5)(4+2)]
By simply counting you can see why more than two intermediate results have to be remembered on the stack just before the last two-number operation (last pair of parentheses), thus overflowing the 4‑level stack. In the following (•) represents one intermediate result on the stack.
We’ll start on the left: after having calculated (3+1)(4+3) there is 1 result on the stack:
(•)+(2+6)(4+6) / ...
Doing (2+6) after this takes 3 stack levels in total (the two new numbers plus the previous result waiting on the stack), and after this addition we have 2 results waiting on the stack:
(•)+(•)(4+6) / ...
Now we can do (4+6), and while doing this operation all 4 stack levels will be in use; after this we can finish the numerator of the division, leaving one result on the stack:
(•) / ...
Because the denominator of the division has the same structure as the numerator, it can easily be seen that at some point in doing the denominator, we’ll have the following situation:
(•) / (•)+(•)(4+2), and finishing that calculation would require 5 stack levels, which is too much for a 4‑level stack calculator: Q.E.D!
By counting in this way you can predict when 4 stack levels will not suffice. If you follow the rule of always doing calculations from the innermost pair of parentheses outwards you will hardly ever encounter such calculations in practice.
But if you do encounter one or if you’re not sure if the 4 levels of your stack will suffice, then using STO and RCL is easy.
In order to save one keystroke ( x y ) if there is a non-commutative operation (–, ÷, yx ) somewhere in the middle of the calculation, start with the part after this operation (in this case the denominator), STOre the intermediate result, and when the part before this operation (the numerator) is done, RCL (recall) the intermediate result and press the middle operation key:
y ) if there is a non-commutative operation (–, ÷, yx ) somewhere in the middle of the calculation, start with the part after this operation (in this case the denominator), STOre the intermediate result, and when the part before this operation (the numerator) is done, RCL (recall) the intermediate result and press the middle operation key:
| Example XXVII: |
|
(3+1)(4+3) + (2+6)(4+6)
|
|
|
(2+3)(2+1) + (3+5)(4+2)
|
* The HP-35 had only one memory location apart from the stack; later models need a register number after STO and RCL.
| Press |
Display |
Comments |
| 2 ENTER↑ 3 + |
5 |
| 2 ENTER↑ 1 + |
3 |
| × |
15 |
| 3 ENTER↑ 5 + |
8 |
| 4 ENTER↑ 2 + |
6 |
| × |
48 |
| + |
63 |
| STO |
63 |
| 3 ENTER↑ 1 + |
4 |
| 4 ENTER↑ 3 + |
7 |
| × |
28 |
| 2 ENTER↑ 6 + |
8 |
| 4 ENTER↑ 6 + |
10 |
| × |
80 |
| + |
108 |
| RCL |
63 |
| ÷ |
1.714285714 |
The important lesson from this example is: remember that at most two intermediate results can be kept on the stack if you still have to enter a new pair of parentheses with a two-number calculation in it, in other words: when you still have to press ENTER↑ at least once!
Appendices
- The Stack
- LAST x
- Percentage calculations
- RPN keeps you in control
- Order of precedence of operators
- Things HP did (and does) not tell in the Manuals of some of their RPN-calculators
- RPN Variants
- Using the UNIX ‘desk calculator’ dc in interactive mode
Appendix A. The Stack
The classical 4-level automatic memory stack consists of four storage locations or registers (called X, Y, Z and T) that can best be seen as arranged one on top of the other, T being the top register, and X the bottom register. The display always shows the number in the X register, unless the calculator is in programming mode.
When you key-in a number, it goes into the X register, and so is displayed. Also the result of the last calculation will be stored into the X register, and so will be visible. Results of previous calculations are automatically stored into the Y, Z and T registers in a last-in-first-out manner.
| T |
0.000 |
|
| Z |
0.000 |
|
| Y |
0.000 |
|
| X |
0.000 |
The X register is always displayed |
In some models (HP‑42S, HP 33s, HP 35s, WP 31S and WP 34S with YDON) also the contents of the Y register is shown in the display, above the contents of the X register, which can be handy in case of non-commutative operations (–, ÷, yx ) to get the order of the two numbers right.
In the HP graphing calculators (HP series 28, 48 and 49, HP 50g and Prime) three or more stack levels are visible in the display.
The HP graphing calculators have much more than four stack levels, numbered from 1 upwards rather than using letters. In all except the Prime the number of stack levels is only limited by the amount of memory; the Prime has a fixed number of 128 stack levels. In this way the chance of stack overflow (loss of the number on the top of the stack) is virtually zero, or in case of the Prime greatly reduced. Another difference is the behaviour of the ENTER key, called ‘Entry RPN’. Even so most of what follows also applies to them. Just think of the X register as the lowest number in the display: either the command/entry line or stack level 1. For details on the differences see Appendix G. RPN Variants.
In the examples below the stack is shown to be filled initially with the numbers 1.0 to 4.0 as the results of previous operations.
One-number calculations
| T |
4.000 |
|
4.000 |
| Z |
3.000 |
|
3.000 |
| Y |
2.000 |
|
2.000 |
| X |
1.000 |
e x |
2.718 |
One-number calculations only act on the number in the X register, and the result overwrites this number. In the example above by pressing the e x key 1.0 is replaced by the (rounded) result of e 1.0. The other stack registers remain the same.
| T |
4.000 |
|
3.000 |
|
3.000 |
| Z |
3.000 |
|
2.000 |
|
2.000 |
| Y |
2.000 |
|
2.718 |
|
2.718 |
| X |
2.718 |
169 |
169.000 |
√x |
13.000 |
When you key-in a new number, e.g. 169, it always goes into the X register, and so is displayed. The numbers in the other stack registers are automatically ‘pushed up’ one level to make room for the new number; the number previously in the T register (4.000) is lost. This ‘pushing up’ of the numbers in the stack when a new number is keyed-in is also called stack lift.
Now when you press another one-number function key, e.g. √x , again the number in the X register is replaced by the result of the function and the other stack registers remain the same.
So remember:
– Pressing a one-number function key only changes the number in the X register; the other stack registers (Y, Z, T) are unaffected.
– When you subsequently key-in a new number this appears in the X register; the result of the previous operation is ‘pushed up’ the stack and thus preserved, and at the same time the contents of the top register T is lost.
Two-number calculations
| T |
|
3.000 |
|
2.000 |
|
2.000 |
|
2.000 |
| Z |
|
2.000 |
|
2.718 |
|
2.000 |
|
2.000 |
| Y |
|
2.718 |
|
13.000 |
|
2.718 |
|
2.718 |
| X |
√x |
13.000 |
12 |
12.000 |
+ |
25.000 |
% |
0.679 |
In the figure above the number in the display (13.000) is the result of a previous operation.
Hence if you now key-in another number, e.g. 12, it is recognized as a new number so the numbers in the stack are automatically ‘pushed up’ one level to make room for the new number; and the number previously in the T register (3.000) is lost.
Two-number functions always act on X and Y, and the result replaces the number in X. For example if you press + then X is added to Y, and the result (25.0 in the above example) is stored in X. Except for percentage functions, in two-number functions the other numbers in the stack are ‘popped down’ one level (also called stack drop) and the contents of T (2.0) is copied to Z.
As you can see in the figure in case of percentage functions (%, ∆% and %T) there is no stack drop: the number in the Y register is preserved and can be used in further operations (see Example VIII and Appendix C for examples of calculations with percentage functions). The percentage functions in the HP graphing calculators do not have this useful feature; there you have to press ENTER twice after the base number to simulate this behaviour.
The above shown two-number functions were done respectively with one newly keyed-in number and one number already on the stack, and with two numbers already on the stack. When you want to do a two-number function with two newly keyed-in numbers you need to use ENTER to separate the two numbers. Apart from this ‘number entry termination’ function, in a Classical RPN machine pressing ENTER has three other immediate effects, as shown in the next figure:
| T |
4.000 |
|
3.000 |
|
2.000 |
|
2.000 |
|
2.000 |
| Z |
3.000 |
|
2.000 |
|
1.000 |
|
1.000 |
|
2.000 |
| Y |
2.000 |
|
1.000 |
|
27.000 |
|
27.000 |
|
1.000 |
| X |
1.000 |
27 |
27.000 |
ENTER↑ |
27.000 |
38 |
38.000 |
+ |
65.000 |
- it duplicates the contents of X into Y, and thereby
- it causes a stack lift
- it then temporarily disables the stack lift, so when the next number is keyed-in it overwrites the number in X and the rest of the stack remains unchanged
This duplicating property of ENTER is the basis for a peculiar way to square numbers, e.g.: 7 ENTER↑ × with result: 49.000. On the HP‑35 this was the standard way to square a number, as there was no key for x2 !
Pressing ENTER to square a number uses one extra stack level, so if your calculator has a separate x2 key it is better to use that.
It is obvious that only two of the four numbers previously on the stack (1.0 and 2.0) are preserved when a two-number function with two newly keyed-in numbers is done; the numbers 3.0 and 4.0 previously on the stack are lost.
ENTER should only be used to separate two numbers keyed-in sequentially without another function in-between. Using ENTER twice (after each number keyed-in) in a Classical RPN calculator gives a false result (without warning!). This is shown in the next example:
| T |
4.000 |
|
3.000 |
|
2.000 |
|
2.000 |
|
1.000 |
|
1.000 |
| Z |
3.000 |
|
2.000 |
|
1.000 |
|
1.000 |
Wrong! |
27.000 |
|
1.000 |
| Y |
2.000 |
|
1.000 |
|
27.000 |
|
27.000 |
⬇ |
38.000 |
|
27.000 |
| X |
1.000 |
27 |
27.000 |
ENTER↑ |
27.000 |
38 |
38.000 |
ENTER↑ |
38.000 |
+ |
76.000 |
← Wrong! |
The answer is wrong because we calculated the result of 38 + 38 and not of 27 + 38.
In the models that use ‘Entry RPN’ — the HP 20b, 30b and the graphing calculators (HP series 28, 48 & 49, HP 50g and HP Prime) — it is allowed to press ENTER↑ (called INPUT on the 20b and 30b) after the second number, but it is not necessary.
Remember:
– ENTER normally should only be used to separate two numbers keyed-in sequentially (without a function key in-between)
– On the classical 4-level stack by pressing ENTER↑ once the results of only two previous operations will be preserved.
Nested parentheses and stack overflow
When you start calculations with nested parentheses at the innermost set of parentheses the stack will not easily overflow.
E.g.: 3 × [4 + (5 × (6 + 7))]
| T |
0 |
|
0 |
|
0 |
|
0 |
|
0 |
|
0 |
|
0 |
|
0 |
|
0 |
|
0 |
|
0 |
| Z |
0 |
|
0 |
|
0 |
|
0 |
|
0 |
|
0 |
|
0 |
|
0 |
|
0 |
|
0 |
|
0 |
| Y |
0 |
|
0 |
|
6 |
|
6 |
|
0 |
|
13 |
|
0 |
|
65 |
|
0 |
|
69 |
|
0 |
| X |
0 |
6 |
6 |
ENTER↑ |
6 |
7 |
7 |
+ |
13 |
5 |
5 |
× |
65 |
4 |
4 |
+ |
69 |
3 |
3 |
× |
207 |
But when you do these calculations from left to right on a 4-level stack then
stack overflow is easily reached and you will get wrong answers (without warning).
E.g.: 3 × [4 + (5 × (6 + 7))] (left-to-right, ↑ stands for ENTER↑ )
| T |
0 |
|
0 |
|
0 |
|
0 |
|
0 |
|
0 |
|
3 |
|
3 |
|
4 |
|
4 |
|
4 |
|
4 |
|
4 |
|
4 |
| Z |
0 |
|
0 |
|
0 |
|
0 |
|
3 |
|
3 |
|
4 |
|
4 |
|
5 |
|
5 |
|
4 |
|
4 |
|
4 |
|
4 |
| Y |
0 |
|
0 |
|
3 |
|
3 |
|
4 |
|
4 |
|
5 |
|
5 |
|
6 |
|
6 |
|
5 |
|
4 |
|
4 |
|
4 |
| X |
0 |
3 |
3 |
↑ |
3 |
4 |
4 |
↑ |
4 |
5 |
5 |
↑ |
5 |
6 |
6 |
↑ |
6 |
7 |
7 |
+ |
13 |
× |
65 |
+ |
69 |
× |
276 |
← Wrong! |
The answer is wrong because the 3 is lost when the ENTER after the 6 is pressed (or when the 7 is pressed in Entry RPN models).
Stack manipulation
In Classical RPN calculators ENTER↑ is used
three times to fill the stack with four numbers:
| T |
0.000 |
|
0.000 |
|
0.000 |
|
0.000 |
|
0.000 |
|
0.000 |
|
4.000 |
|
4.000 |
| Z |
0.000 |
|
0.000 |
|
0.000 |
|
0.000 |
|
4.000 |
|
4.000 |
|
3.000 |
|
3.000 |
| Y |
0.000 |
|
0.000 |
|
4.000 |
|
4.000 |
|
3.000 |
|
3.000 |
|
2.000 |
|
2.000 |
| X |
0.000 |
4 |
4.000 |
ENTER↑ |
4.000 |
3 |
3.000 |
ENTER↑ |
3.000 |
2 |
2.000 |
ENTER↑ |
2.000 |
1 |
1.000 |
Important! When you would press ENTER↑ a fourth time after the fourth number then the first number (4.0) will be lost*:
* Except in the above mentioned HP 20b/30b ‘Entry RPN’ calculators, where you do have to press ENTER↑ four times to fill the 4-level stack.
| T |
4.000 |
|
3.000 |
| Z |
3.000 |
|
2.000 |
| Y |
2.000 |
|
1.000 |
| X |
1.000 |
ENTER↑ |
1.000 |
The key x y is called X exchange Y. In some RPN calculators a similar function is called SWAP. The story of SWAP is slightly confusing, but don’t get discouraged and read on. In the HP 20b/30b this is the
y is called X exchange Y. In some RPN calculators a similar function is called SWAP. The story of SWAP is slightly confusing, but don’t get discouraged and read on. In the HP 20b/30b this is the  symbol on the
symbol on the  key, which functions identical to x
key, which functions identical to x y when in RPN mode.
In the HP 28 series SWAP is the shifted function of the
y when in RPN mode.
In the HP 28 series SWAP is the shifted function of the  (Backspace) key. In graphing calculators that have a separate right arrow key ► (HP 48 and 49 series and HP 50g) this key performs the SWAP function, but only when there’s no command line; so sometimes you have to press ENTER before SWAP ( ► ). In the HP Prime the SWAP function
(Backspace) key. In graphing calculators that have a separate right arrow key ► (HP 48 and 49 series and HP 50g) this key performs the SWAP function, but only when there’s no command line; so sometimes you have to press ENTER before SWAP ( ► ). In the HP Prime the SWAP function  is under the comma key
is under the comma key  , but only when the entry line is empty; so here too sometimes you have to press ENTER before SWAP (
, but only when the entry line is empty; so here too sometimes you have to press ENTER before SWAP (  ).
).
These keys are used to exchange the contents of the lowest two stack registers (classically called X and Y), which can be very handy to get the order of numbers right before a non-commutative operation –, ÷ or y x when you do this operation backwards, i.e. from right to left in stead of from left to right (see Examples XVI-XVIII):
| T |
4.000 |
|
4.000 |
| Z |
3.000 |
|
3.000 |
| Y |
2.000 |
|
1.000 |
| X |
1.000 |
x y y |
2.000 |
Stack inspection
Pressing x y twice leaves the stack unchanged, so in this way the contents of Y can be inspected:
y twice leaves the stack unchanged, so in this way the contents of Y can be inspected:
| T |
4.000 |
|
4.000 |
|
4.000 |
| Z |
3.000 |
|
3.000 |
|
3.000 |
| Y |
2.000 |
|
1.000 |
|
2.000 |
| X |
1.000 |
x y y |
2.000 |
x y y |
1.000 |
R↓ (called roll down) ‘rotates’ the contents of all four stack registers. Pressing this key four times lets you inspect the content of Y, Z, T and finally X again:
| T |
4.000 |
|
1.000 |
|
2.000 |
|
3.000 |
|
4.000 |
| Z |
3.000 |
|
4.000 |
|
1.000 |
|
2.000 |
|
3.000 |
| Y |
2.000 |
|
3.000 |
|
4.000 |
|
1.000 |
|
2.000 |
| X |
1.000 |
R↓ |
2.000 |
R↓ |
3.000 |
R↓ |
4.000 |
R↓ |
1.000 |
Of course in calculators with five or eight or more stack levels R↓ ‘rotates’ the contents of all 5 or 8 or all occupied stack levels. In HP graphing RPN calculators similar but somewhat different functions are ROLL and ROLLD. Read the manuals for details.
Repeated calculations with a constant
When the numbers in the stack drop while doing a two-number operation the number in the T register remains constant and is copied to the next lower level. Because stack drop is also known as ‘popping the stack’ this is sometimes called Top copy on pop. Of course this only works when there is an upper limit to the stack. This property of RPN calculators with a limited stack can be used to do calculations with a constant.
Example XXVIII: If your firm has a projected
growth rate in sales of 17% per year, when will the sales have doubled?
Solution: 17% per year makes an annual growth factor of 1.17. Let the current
sales be 100.
* In the Entry RPN calculators HP 20b and HP 30b ENTER↑ should be pressed four times to fill the 4-level stack with four numbers.
| Press |
Display |
Comments |
| 1.17
|
1.17 |
|
ENTER↑
ENTER↑
ENTER↑
|
1.17 |
| 100 |
100.00 |
| × |
117.00 |
| × |
136.89 |
| × |
160.16 |
| × |
187.39 |
| × |
219.24 |
So within 5 years the sales will have doubled, given this constant growth rate.
Appendix B. LAST x
The first two HP calculators (the HP-35 and 80) did not have one, but all later Classical RPN calculators have a LAST X register, which automatically holds the contents of the X register just before the most recent operation. Pressing LAST x recalls this value into the X register. In the HP 20b and 30b the LAST x function is called ANS. In the WP 34S the LAST x function is performed by RCL L (= RCL EEX ).
The WP 31S doesn’t have a LAST x function but instead features UNDO , which restores the stack and all other registers to the state they were before the last command.
The HP graphical calculators have a LAST or LAST ARG or ANS function which serves a similar purpose, but recalls all arguments of the last operation to the stack.
These keys can be used to correct entry mistakes or to reuse a number in a calculation.
Use of LAST x to correct entry mistakes
One-number functions
If you pressed the wrong one-number function key, use LAST x to recall the number so you can press the correct function key.
E.g. In a long calculation you pressed e x by mistake, but wanted to press 10 x. You don’t have to start all over again!
First delete the wrong result with CL x or  to prevent that it is saved on the stack.
to prevent that it is saved on the stack.
Retrieve the number that was in the X register before the mistake and press the correct function key: LAST x 10 x
Two-number functions
Wrong function or wrong second number.
Correct mistakes while keying in two-number functions with LAST x and the inverse of the function you used (+ vs. – or × vs. ÷). This brings back the state of the stack just before the mistake; then you can correct it. Use of CL x or  is only necessary if you’re in the middle of a long calculation to prevent that the wrong number is put on the stack.
is only necessary if you’re in the middle of a long calculation to prevent that the wrong number is put on the stack.
E.g. you want to calculate 65 × 32
You can make three kinds of mistakes:
|
| Mistake |
|
Correction
|
|
65 ENTER↑ 32 +
|
(wrong function) |
(  )
LAST x – )
LAST x –
|
|
|
(  )
LAST x × )
LAST x × |
|
65 ENTER↑ 332 × |
(wrong second number) |
(  ) LAST x ÷ ) LAST x ÷
|
|
|
32
×
|
|
665 ENTER↑ 32 ×
|
(wrong first number) |
(  ) 65 LAST x × ) 65 LAST x ×
|
Use of LAST x to reuse a number
There are two situations where this can be handy:
-
In a longer calculation where the same number appears twice with only one operation in-between:
(567.89012 + 1.23456789) ÷ 1.23456789
567.89012 ENTER↑
1.23456789 +
LAST x
÷
Answer: 460.9910014
-
In a repeating short calculation as a semi-automatic constant.
E.g.: the price of an item is € 123.25; what would be the cost of 7, 13 or 17 of these items?
Enter the constant last:
7 ENTER↑ 123.25 ×
Cost: 862.75
13 LAST x ×
Cost: 1,602.25
17 LAST x ×
Cost: 2,095.25
Appendix C. Percentage calculations
Percentage functions (%, ∆% and %T) are a bit special because in many RPN calculators the first (base) number is preserved during the operation and can be used in further calculations. In some (notably the RPN graphing) calculators the base number is not preserved; there you’ll have to press ENTER two times between the base and the percentage number to get the same effect. Also in the RPN graphing calculators the designations of these functions may differ: ∆% may be called %CH or %CHANGE and %T may be called %TOTAL.
Example XXIX: A car is listed for $29,690. You deal a 7% discount and the sales tax is 9.5%. What will be the total purchase price?
* In RPN graphing calculators press ENTER↑ twice!
† In RPN graphing calculators here you’ll have to press ENTER↑ to duplicate this result before keying-in the percentage and pressing %
| Press |
Display |
Comments |
| 29690 |
29,690 |
| ENTER↑ |
29,690.00 |
| 7 |
7 |
| % |
2,078.30 |
| – |
27,611.70 |
| 9.5 |
9.5 |
| % |
2,623.11 |
| + |
30,234.81 |
Example XXX: ∆% calculates the percent change between two numbers, negative if the second is lower than the first. Because the base number is saved you can easily make multiple comparisons.
E.g.: Yesterday the stock price of a share fell from 61¾ to 53½. What is the percent change? And what if the price rose to 65 or 70?
* In RPN graphing calculators press ENTER↑ twice!
| Press |
Display |
Comments |
| 61.75 |
61.75 |
| ENTER↑ |
61.75 |
| 53.50 |
53.50 |
| ∆% |
–13.36 |
| CL x |
0.00 |
| 65 |
65.00 |
| ∆% |
5.26 |
| CL x |
0.00 |
| 70 |
70.00 |
| ∆% |
13.36 |
Example XXXI: Goods are purchased for a wholesale price of $22 and sold for a retail price of $29.99. What is the markup (price difference as a percentage of cost price (wholesale price)) and what is the margin (price difference as a percentage of selling price (retail price)?
* In RPN graphing calculators press ENTER↑ twice!
| Press |
Display |
Comments |
| 22 |
22. |
| ENTER↑ |
22.00 |
| 29.99 |
29.99 |
| ∆% |
36.32 |
| LAST x |
29.99 |
| 22 |
22.0 |
| ∆% |
–26.64 |
| CH S |
26.64 |
Example XXXII: %T calculates what percentage of a total a certain part of that total is. E.g. in a population there are 356 men, 401 women and 289 children. What percentage of the total population do the three numbers account for?
| Press |
Display |
Comments |
| 356 |
356 |
| ENTER↑ 401 |
401 |
| + |
757 |
| 289 + |
1,046 |
| 356 |
356 |
| %T |
34 |
| CL x 401 |
401 |
| %T |
38 |
| CL x 289 |
289 |
| %T |
28 |
The behaviour of the stack in percentage functions is described here.
Appendix D. RPN keeps you in control
If you let your ‘algebraic’ calculator or spreadsheet computer program decide over the operator precedence of a calculation you might not get the right answer. The most notorious example is a calculation like 6 : 2 × (1 + 2), which is interpreted differently by Casio and TI (see Appendix E to find out which one is right):

Another example is the treatment of the unary minus as having a higher precedence than exponentiation by Microsoft’s spreadsheet application Excel, which contends that ‑32 = (‑3)2 = 9 whereas the correct answer is: ‑32 = ‑(32) = ‑9
Also Excel evaluates 432 (written as 4^3^2) as (43)2 = 642 = 4096. The usual interpretation of 432 is to work from the top down, so there are implied parentheses in the exponent: 432 = 4(32) = 49 = 262,144
Because in RPN the order of operations is not decided by the calculator but by the user it is wise to brush-up on this important issue (see the next Appendix).
Appendix E. Order of precedence of operators
An RPN calculator won’t do it for you, so it is important that you have the simple rules of mathematical operator precedence in your head.
The standard order of operations is as follows:
- Parentheses (brackets)
- Exponents and roots
- Multiplication and division
- Addition and subtraction
Mnemonic: PEMA!
N.B.: Operations that are on the same line in the above list, such as addition and subtraction or multiplication and division, have equal precedence. Mixed operations with equal precedence (e.g. a series of additions and subtractions or several multiplications and divisions next to each other) are evaluated from left to right.
What is the correct way to calculate 6 : 2 × (1 + 2) ?
Because multiplication and division have the same operator precedence, when next to each other they should be evaluated from left-to-right:
6 : 2 × (1 + 2) =
3 × (1 + 2) =
3 × 3 = 9
It may help to remember that division by 2 is the same as multiplication by ½ because then it is easier to do the same calculation backwards:
6 : 2 × (1 + 2) =
6 × ½ × 3 =
6 × 1.5 = 9
Another correct way is thus:
6 : 2 × (1 + 2) =
(6 : 2 ) × (1 + 2) =
(6 : 2 ) × 3 =
3 × 3 = 9
It is wrong to do it like this:
6 : 2 × (1 + 2) =
6 : (2 × (1 + 2)) =
6 : (2 × 3) =
6 : 6 = 1 (wrong!)
Using an RPN calculator this calculation can be done in several ways:
6
ENTER↑
2
÷
1
ENTER↑
2
+
×
or
1
ENTER↑
2
+
2
1/x
×
6
×
or
1
ENTER↑
2
+
2
ENTER↑
6
x y
÷
×
y
÷
×
or
1
ENTER↑
2
+
6
ENTER↑
2
÷
×
All give the same result:9
How to apply the unary minus operator?
‑32 = ‑(32) = should be calculated on an RPN calculator like so:
3
ENTER↑
2
y x
CH S
Result:‑9
When negating a number it is important to always press CH S after keying-in the number and before pressing ENTER↑. For a discussion of why this is important read this article.
What is the correct way to calculate 432 ?
Using an RPN calculator this calculation can be done in two ways:
4
ENTER↑
3
ENTER↑
2
y x
y x
or
3
ENTER↑
2
y x
4
x y
y x
y
y x
Both give the same result:262,144 (see Examples XVIII and XIX)
Appendix F. Things HP did (and does) not tell in the Manuals of some of their RPN-calculators
Left-to-right or from within the innermost parentheses?
The HP‑35 Operating Manual (1972) concludes with an RPN algorithm and flow chart ‘adequate for most practical problems’. Because it says to key-in the numbers ‘in the order in which they occur’ (that is from left to right) this algorithm fails in some quite simple calculations with nested parentheses (e.g. see Example XIV above).
The same algorithm and a similar flow chart were given in the HP‑45 Owner’s Handbook (1973). Later HP published a brochure titled ‘ENTER↑ vs. =’, which was devoted solely to the basics of RPN calculators as opposed to Algebraic notation calculators. This brochure contained a simplified version of the flow chart, having the same flaw. It was the last time HP used this flow chart (as far as I know), although the algorithm it depicts is perfectly valid in the later RPL calculators with (virtually) unlimited stack length.
In the manuals of all other early RPN Calculators (HP-80, 70, 65, 55) this advise is given: ‘Almost all problems can be solved (...) from left-to-right.’ But it was left as an exercise to the user to figure out when a problem could not be solved this way, and how then to proceed.
Only several calculator models later, in the Owner’s Handbook of the HP‑25 (1975) can we read ‘It is best to start every problem at its innermost number or parentheses and working outward.’ Since then a similar advise is given in the Handbook of every next model. But even at the present day the HP‑12C and HP‑12C Platinum User’s Guides give this advise only in an appendix.
Use of SWAP
Until 1983 the use of x y in nested calculations when you have to do a non-commutative operation (–, ÷, yx ) ‘backwards’ was only hinted at in every manual. Starting with the HP‑41CX Manual (1983) this point is worked out more explicitly. But even in 2014 the current versions of the HP‑12C and HP‑12C Platinum User’s Guides do not mention this important point, not even in the Appendix about the stack. In the later graphical calculators (HP‑49 series and HP‑50g) the use of ► for the SWAP function is hardly documented in the Manuals and the function is not printed on the keyboard.
y in nested calculations when you have to do a non-commutative operation (–, ÷, yx ) ‘backwards’ was only hinted at in every manual. Starting with the HP‑41CX Manual (1983) this point is worked out more explicitly. But even in 2014 the current versions of the HP‑12C and HP‑12C Platinum User’s Guides do not mention this important point, not even in the Appendix about the stack. In the later graphical calculators (HP‑49 series and HP‑50g) the use of ► for the SWAP function is hardly documented in the Manuals and the function is not printed on the keyboard.
Stack Overflow
The gravest omission in the User’s documentation of every single HP classical 4-level stack RPN calculator up to the present day is the failure to mention the possibility of stack overflow. Nowhere is it mentioned explicitly that sometimes wrong answers are given without warning.
And conflicting information is given about the number of intermediate results that are preserved on the 4-level stack in various manuals. The HP‑55 Owner’s Handbook (1975) states that ‘up to four intermediate results are stored in the stack’ (italics are mine); using the same example the HP‑31 Owner’s Handbook (1978) says ‘the automatic memory stack stores up to three intermediate results until you need them, and then inserts them into your calculation’. Not even in the newest HP Manual is it admitted that quite often only two intermediate results are preserved, specifically when you have to use ENTER↑ once again, e.g. to put two new numbers on the stack.
In the opinion of the author of this RPN Tutorial this failure by HP to mention the obvious limitation of the 4-level stack and its consequences explicitly has done the acceptance of RPN more harm than good.
Appendix G. RPN variants
Often the two main variants of RPN are referred to as ‘Classical RPN’ and ‘RPL’. This is a bit confusing because RPL is actually the name of the programming language used in the HP graphing calculators of series 28, 48 & 49 and also in the HP 50g. The HP Prime has another programming language but uses a similar variant of RPN.
Purely looking at the workings of the stack of RPN calculators (and not at their programming capabilities) a few RPN variants can be discerned. Both the bottom and the top of the stack may vary.
A. Bottom of the stack:
1. Classical RPN
2. Entry RPN
B. Top of the stack:
1. Small stack (4-, 5- or 8-level) with ‘top copy on pop’
2. Very large stack (>100 levels), no ‘top copy on pop’
Four types of RPN
All four possible combinations of the 2 × 2 possibilities of RPN variants actually do exist, although not always in hardware:
-
The combination of Classical RPN with a small stack and ‘top copy on pop’ is well known. Besides the 4-level stack of all classical HP RPN calculators (all HP RPN calculators except those listed below after β. and γ.) and their emulations there is the 5-level stack of the Heathkit OC-1401, and the 8-level mode of the WP 31S and WP 34S.
-
All HP RPN graphing calculators (series 28, 48 & 49, the HP 50g and Prime) have Entry RPN and an unlimited or very large stack (128 stack levels in the Prime). Also the UNIX command-line ‘desk calculator’ dc has an unlimited stack and uses Entry RPN.
-
The HP 20b and HP 30b have Entry RPN and a 4-level stack with ‘top copy on pop’.
-
The Calculator application in macOS in RPN-mode combines Classical RPN behaviour of the ENTER key with an unlimited stack.
The Bottom of the stack: Classical RPN versus Entry RPN
The differences at the bottom of the stack need not bother you as long as you stick to the rules given in the ‘Cheat Sheet’. Especially observe the rule to use ENTER↑ only to separate two numbers that have to be keyed in immediately one after the other. When you can’t see the stack do not uncritically rely on ENTER↑ to duplicate a number on the stack and do not use ENTER↑ to ‘enter’ a number into the stack.
There are two important exceptions to this latter rule worthwhile to remember, which only apply to the HP graphing calculators (so it’s easy to use them because you can see the stack):
-
In most HP graphing calculators SWAP only works when the command line / entry line is empty, so often it will be necessary to press Enter before ► or
 (
(  ) when you want to exchange the lowest two stack levels.
) when you want to exchange the lowest two stack levels.
-
% functions in HP graphing calculators do not automatically preserve the base (first) number like in other HP RPN calculators, so when you want to use that number in further calculations (e.g. to add a percentage) you will have to press Enter twice between the base and the percent to duplicate the base number.
If you want to know what’s happening on the stack in Classical RPN and Entry RPN then the following is some explanation.
3
4
——— +
7
| Classical RPN: |
3
ENTER↑
4
|
+ |
Answer: 7 |
|
3
ENTER↑
4
ENTER↑
|
+ |
Answer: 8 (wrong!) |
| Entry RPN: |
3
ENTER↑
4
|
+ |
Answer: 7 |
|
3
ENTER↑
4
ENTER↑
|
+ |
Answer: 7 |
So Entry RPN is more forgiving, because you cannot do it wrong!
Here in Appendix A can you see how the wrong answer in Classical RPN calculators is produced.
In practice the difference between Classical RPN and Entry RPN is of no importance as long as you stick to the rule to use ENTER↑ only to separate two numbers that have to be keyed in immediately one after the other and not to ‘enter’ a number into the stack.
The mechanism of this difference on the stack can easily be seen in the following figures.
The first key sequence above (plus an extra ENTER↑ ) on a Classical RPN calculator:
| T |
0.000 |
|
0.000 |
|
0.000 |
|
0.000 |
|
0.000 |
|
0.000 |
| Z |
0.000 |
|
0.000 |
|
0.000 |
|
0.000 |
|
0.000 |
|
0.000 |
| Y |
0.000 |
|
0.000 |
|
3.000 |
|
3.000 |
|
0.000 |
|
7.000 |
| X |
0.000 |
3 |
3.000 |
ENTER↑ |
3.000 |
4 |
4.000 |
+ |
7.000 |
ENTER↑ |
7.000 |
As you can see in the above figure in Classical RPN:
- ENTER↑ always duplicates X into Y (after number entry and after pressing a function key).
- But when followed by a next number entry the duplication is neutralized because the number in the X register is overwritten! This function of the ENTER key is also known as ‘temporary stack lift disable’.
Remember: in Classical RPN calculators if ENTER↑ is not followed by a number you always have the number twice on the stack.
Now the same key sequence on the HP Prime, which has Entry RPN:
| …: |
|
|
|
|
|
|
|
|
|
|
|
| 5: |
|
|
|
|
|
|
|
|
|
|
|
| 4: |
|
|
|
|
|
|
|
|
|
|
|
| 3: |
|
|
|
|
|
|
|
|
|
|
|
| 2: |
|
|
|
|
|
|
|
|
|
|
7.000 |
| 1: |
|
|
|
|
3.000 |
|
3.000 |
|
7.000 |
|
7.000 |
| Entry line |
|
3 |
3 |
ENTER↑ |
|
4 |
4 |
+ |
|
ENTER↑ |
|
In Entry RPN pressing ENTER sometimes moves and sometimes duplicates:
- In graphing calculators it is easy: if the command/entry line is empty ENTER duplicates else it moves.
- In other Entry RPN calculators remember: if ENTER is pressed after ENTER or after a function key then you have the number twice on the stack, even if followed by a number entry.
- Duplication in Entry RPN is never neutralized!
The Top of the stack: Small versus very large/‘unlimited’ stack. ‘Top copy on pop’
The height of the stack is important to know for all users because a small stack always leaves open the possibility of stack overflow, while in manual operation a very large stack is virtually immune to this error. Items 5. 6. & 7. of the ‘Cheat Sheet’ give hints on how to prevent stack overflow in calculators with a small stack.
The other difference at the top of the stack that might be important is the presence or absence of top copy on pop, which is only present in small stack models. See Example XXVIII. In calculators with an very large stack you can somewhat emulate this behaviour by pressing Enter several times to replicate the constant number into the stack.
Which type of RPN does my calculator have?
To determine if your RPN calculator has Classical RPN or Entry RPN behaviour of the bottom of the stack do the following test.
First bring the stack in a consistent pre-condition by pressing:
0 ENTER↑ 0 ENTER↑
Then press:
5 ENTER↑ ×
If the result is 25 then your calculator has Classical RPN behaviour of the ENTER key.
If the result is 0 then your calculator has Entry RPN behaviour of the ENTER key.
The stack size should be evident from the documentation. But if you don't have that information you could do the following test.
First press:
0 ENTER↑ 0 ENTER↑
Then press:
1 ENTER↑ 2 ENTER↑ 3 ENTER↑ 4 ENTER↑ 5 ENTER↑
6 ENTER↑ 7 ENTER↑ 8 ENTER↑ 9 ENTER↑ (don’t forget the last ENTER!)
Then press 8 times +
• If the result is 45 then the calculator has more than eight stack levels (possibly an unlimited number) and Entry RPN (β-type).
• If the result is 53 then the calculator has more than eight stack levels (possibly an unlimited number) and Classical RPN (δ-type).
• If the result is 54 then the calculator has an 8-level stack and Classical RPN (α-type).
• If the result is 60 then the calculator has a 4-level stack and Entry RPN (γ-type).
• If the result is 63 then the calculator has a 5-level stack and Classical RPN (α-type).
• If the result is 68 then the calculator has a 4-level stack and Classical RPN (α-type).
• If the result is 81 then you have a calculator of the HP 9100 or 9800 series.
The results for the small stack sizes assume that on stack drop the top level copies its contents to the next lower level (‘Top copy on pop’).
Some specific models
The HP RPN graphing calculators
How different is RPN in the HP graphing calculators? Apart from their virtually unlimited stack the only three important dissimilarities are:
-
A slightly different behaviour of the ENTER key: in these calculators ENTER may (but doesn’t need to) be used after each number keyed-in to get it on the stack, so it is allowed to be used like an Enter-key on a computer keyboard.
This postfix use of the ENTER key is also allowed in the HP 20b and HP 30b (that aren’t graphing calculators and do have a 4-level stack; in these models the ENTER key is labelled INPUT). In an article in HP Solve (# 27 p. 42) Richard Nelson calls this possibly postfix use of the ENTER / INPUT key ‘Entry RPN’, as opposed to the compulsory prefix use of ENTER in ‘Classical RPN’.
In ‘Classical RPN’ ENTER is normally only allowed to be used to separate two numbers keyed-in without pressing an operation key in-between. So it is used like the E EX key (‘Enter Exponent’), which also is pressed before keying-in the exponent. This almost exclusive prefix use of the Classical RPN ENTER key could be expressed more clearly if it were labelled E NXT or E NXT # or E NN (for ‘Enter Next Number’) or simply ENTER: .
-
The use of an unnumbered command line (called entry line in the HP Prime) while keying in a new number, which allows to edit the number conveniently. When you press ENTER or a function key the number or the result is placed in stack level 1, and the command line disappears. The command line can be regarded as a temporary ‘stack level 0’. So the lowest stack level (called X in classical RPN) alternates between the command line and level 1 of the stack. In the examples below think of the number in the X register as being on the lowest stack level (either on the command line, ‘level 0’, or on stack level 1). In RPL calculators the command line has more advanced uses that are beyond the scope of this tutorial.
-
SWAP is not always available as a primary key function. When the command line is not visible a SWAP of level 1 and 2 of the stack is done by just pressing ► on the calculators that have this key (HP 48 and 49 series and HP 50g) or pressing  (the comma key
(the comma key  ) on the HP Prime. When the command line is visible just press ENTER to copy the contents of the command line to stack level 1 before pressing ► or
) on the HP Prime. When the command line is visible just press ENTER to copy the contents of the command line to stack level 1 before pressing ► or  .
In the HP series 48 calculators when the command line is visible you may press the left shift key before pressing the ► key to SWAP what is on the command line with level 1 of the stack. In the HP 28 series SWAP is the shifted function of the
.
In the HP series 48 calculators when the command line is visible you may press the left shift key before pressing the ► key to SWAP what is on the command line with level 1 of the stack. In the HP 28 series SWAP is the shifted function of the  (Backspace) key.
(Backspace) key.
The WP 31S and WP 34S
A special case are the new WP 31S and WP 34S calculators, that are not produced by HP but are community-created products based on reprogrammed and relabeled HP 20b or HP 30b hardware. These calculators have the optional use of an 8-level stack and have classical behaviour of the ENTER key. The additional stack levels are called A, B, C and D.
The HP 9100 and HP 9800
A very special case are the first RPN calculators produced by HP, the tabletop models of series 9100 and 9800. They had a 3-level stack and would qualify as Classical RPN according to the first test. But the RPN was quite different. More on this on the pages of the Museum of HP Calculators. It is interesting to note that these early calculators already had a kind of ‘pseudo Entry line’: all input went into the lowest x keyboard register; pressing the ↑ (Enter) key copied this value to the y accumulator register. The results of two-number operations went into this same accumulator, but results of one-number functions went into the x keyboard register. Intermediate results were pushed automatically into the z temporary register, but there was no automatic stack drop. Fortunately the contents of all three registers were visible in the display.
Appendix H. Using the UNIX ‘desk calculator’ dc in interactive mode
dc originally was an arbitrary precision integer arithmetic package. By default the division (/) and square root (v) operations only show rounded integer results, so when trying to get an approximation of √2 by typing: 2vp⏎ the result might be 1; to get a more precise value type the desired number of decimals followed by k (the ‘scale factor’ or ‘precision’) and try again, e.g.: 16k2vp⏎
Now the result should look more familiar: 1.4142135623730950
A few more tips:
-
To separate two numbers keyed-in before an operator type ⏎ (return/enter) or a space.
-
For a negative value first type _ (underscore) and then the number; the - (minus) can only be used to subtract two numbers.
-
Don’t forget to type p⏎ to see the result of an operation (the top-of-stack value).
-
To see all numbers on the stack use f (‘full stack’). Note: f shows a ‘push down stack’ (most recently pushed number shown on top), whereas HP visualizes the stack as a ‘push up stack’ (most recently pushed number shown at the bottom); don't get confused by that!
-
To clear all numbers from the stack use c.
-
To swap the upper two levels of the stack use r (‘reverse’).
-
To duplicate the top-of-stack value to the second stack level use d. In dc typing ⏎ never duplicates.
-
To quit dc use q.
-
dc’s exponentiation (^) only works for integer exponents.
-
Scientific notation with exponents of ten (like ‘367E9’) is not supported.
-
Percentage calculations are not supported. The % symbol is used for the remainder function.
-
dc is a whole programming language. If you would like to know more see this webpage, which is more informative than most man pages.
 y or ► or
y or ► or  in nested calculations. To get the order of the numbers right when you have to do a non-commutative operation (–, ÷, yx ) ‘backwards’, just before pressing the operation key press x
in nested calculations. To get the order of the numbers right when you have to do a non-commutative operation (–, ÷, yx ) ‘backwards’, just before pressing the operation key press x y (‘exchange x and y’). In the HP 20b/30b this is the
y (‘exchange x and y’). In the HP 20b/30b this is the
 key. In HP graphing calculators use SWAP: before the operation key press ENTER followed by ► or
key. In HP graphing calculators use SWAP: before the operation key press ENTER followed by ► or
 (
(  ).
). y
– 3 × Result:–183
y
– 3 × Result:–183
 y, so you save one keystroke.
y, so you save one keystroke.
 in nested calculations.
in nested calculations.
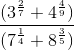 If you’re not sure that this one can be done on a 4-level stack, use
If you’re not sure that this one can be done on a 4-level stack, use 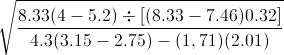
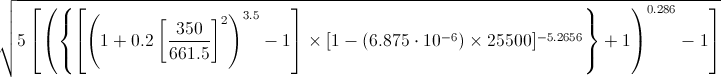

 ) on the
) on the